Engineering
ABS Modelling
MATLAB & Simulink
Control Theory
Vehicle Dynamics
ABS Modelling

Developed a tire model to simulate longitudinal dynamics of a vehicle. This was part of the Vehicle Dynamics class I took at university.

First a model for slip was created using the Pacejka model.

μ(k)=c1⋅(1−e−c2⋅k)−c3⋅k\mu(k) = c_{1}\cdot (1- e^{-c_2 \cdot k}) - c_3\cdot k

Where kk is the braking slip ratio, c1c_1 is the asymptote of the curve, c2c_2 is the shape factor, and c3c_3 is the curvature factor.

The Pacejka model was then used to create a model for the longitudinal force of the tire.

Using newton's second law, on the vehicle body:

m⋅x¨=−FB−FLFL=cw⋅A⋅ρ2⋅x˙2∴FB=−m⋅x¨−cw⋅A⋅ρ2⋅x˙2\begin{align*} m \cdot \ddot{x} &= -F_B - F_L \\ F_L &= c_w \cdot A \cdot \frac\rho2 \cdot \dot{x}^2 \\ \therefore F_B &= - m \cdot \ddot{x} - c_w \cdot A \cdot \frac\rho2 \cdot \dot{x}^2 \\ \end{align*} Wherem:mass of the vehiclex¨:acceleration of the vehicleFB:braking forceFL:drag forcecw:drag coefficientA:frontal area of the vehicleρ:density of airx˙:velocity of the vehicle\begin{align*} Where \\ m &: \text{mass of the vehicle} \\ \ddot{x} &: \text{acceleration of the vehicle} \\ F_B &: \text{braking force} \\ F_L &: \text{drag force} \\ c_w &: \text{drag coefficient} \\ A &: \text{frontal area of the vehicle} \\ \rho &: \text{density of air} \\ \dot{x} &: \text{velocity of the vehicle} \\ \end{align*}

Similarly using newton's second law on the wheel:

JW⋅θ¨w=FB⋅rw−MBFB=μ(k)⋅FNFN=m⋅gk=x˙−rw⋅θ˙wx˙\begin{align*} J_W \cdot \ddot{\theta}_{w} &= F_B \cdot r_w - M_B \\ F_B &= \mu(k) \cdot F_N \\ F_N &= m \cdot g \\ k &= \frac{\dot{x} - r_w \cdot \dot{\theta}_{w} }{\dot{x}} \\ \end{align*} WhereJW:moment of inertia of the wheelθ¨w:angular acceleration of the wheelMB:braking torquerw:radius of the wheelFN:normal forceg:acceleration due to gravity\begin{align*} Where \\ J_W &: \text{moment of inertia of the wheel} \\ \ddot{\theta}_{w} &: \text{angular acceleration of the wheel} \\ M_B &: \text{braking torque} \\ r_w &: \text{radius of the wheel} \\ F_N &: \text{normal force} \\ g &: \text{acceleration due to gravity} \\ \end{align*}

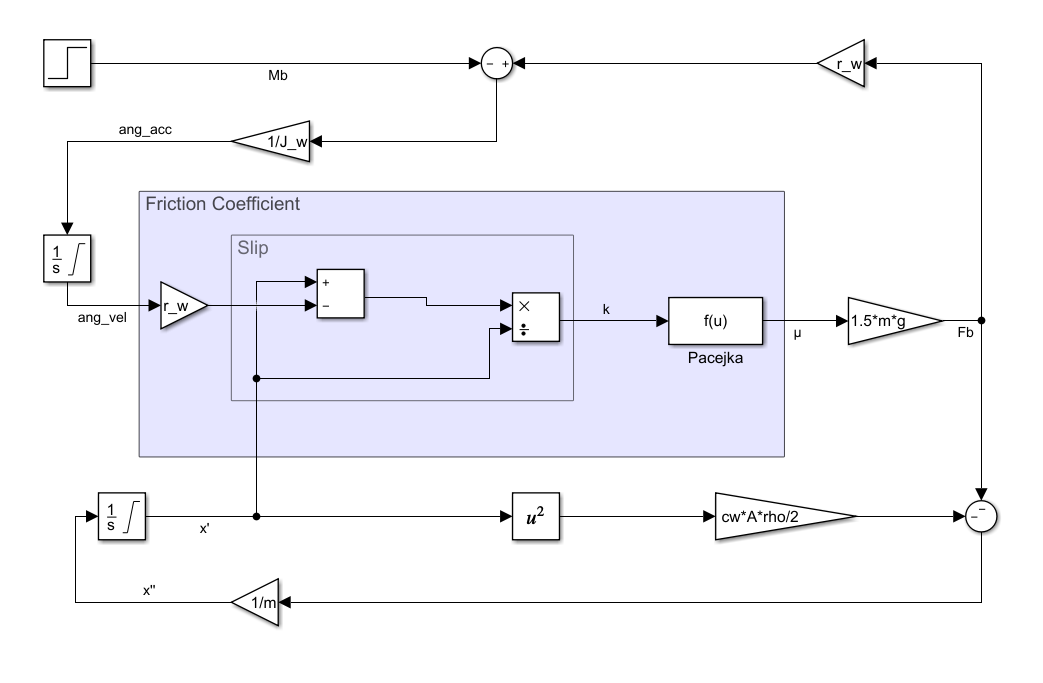
These relationships can be modeled in Simulink as shown below:

abs braking

This model was used as a basis for the ABS system. The system simply compares the slip with an ideal slip parameter and changes the applied dynamic braking torque.

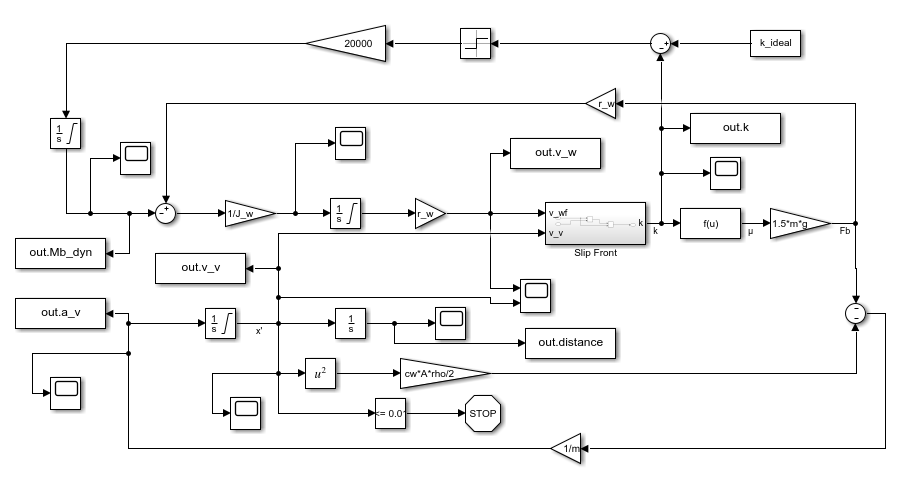
abs_model

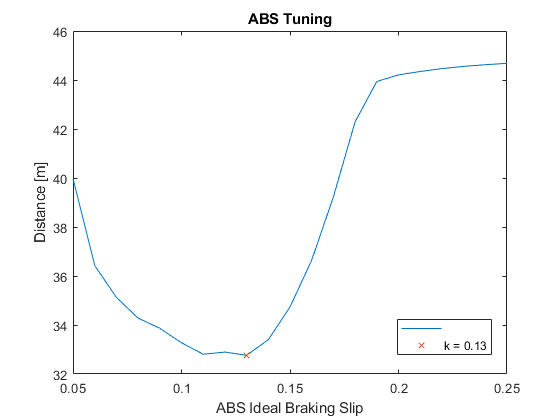
This model was used to find an ideal slip parameter for the vehicle. The ideal slip parameter was found to be 0.13. 

%% Program
close all
clear all
param;

k = 0.05:0.01:0.25;
for i = 1:21
    k_ideal = k(i);
    out = sim('brakingabs.slx');
    D(i)=out.distance(end);
end

[MIN,IND]=min(D);

figure(1)
plot(k,D)
hold on
xlabel('ABS Ideal Braking Slip')
ylabel('Distance [m]')
title('ABS Tuning')
plot(k(IND),D(IND),'x')
legend('','k = 0.13')
hold off

abs = sim('brakingabs.slx');
noabs = sim('braking.slx');

%plots
%...

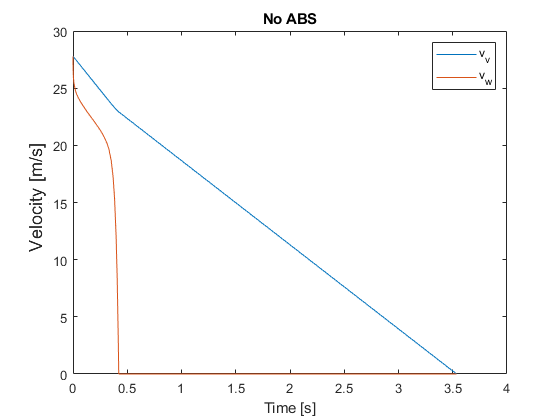
The following graphs show the performance of the ABS function.

abs 1 abs 2 abs 3 abs 4 abs 5